Réflexions du Miroir

Les nombreux logiciels générateurs de fractales permettaient de reprendre, ensuite, un détail de l'image formée et, avec lui, recommencer à nouveau le calcul de la fonction, point par point, par itérations et reproduire le même dessin plus loin en zoomant sur lui. La formule, la plus simple  Z = z² +c, donne déjà des résultats intéressants en partant dans toutes les directions pour s'évader dans un décor qui tend vers l'infini.

La représentation des fonctions fractales est devenue une véritable passion pour beaucoup de possesseurs de PC, un véritable art de l'image s'en est suivi. Il s'est retrouvé sur les murs de beaucoup d'entreprises et de particuliers comme un symbole de beauté et de modernité.

Qui oserait dire que les mathématiques et les nombres ne peuvent pas faire rêver?

Le monde du complexe et du chaos qui l'accompagne, a toujours intrigué les scientifiques pour le recaser dans plus d'ordre sous l'uniformité de quelques formules que l'on espère les plus courtes possibles.

Dès 1812, Simon de Laplace affirmait arbitrairement que si on connaissait la position de toutes les particules de l'univers avec les forces qui les animent, à un instant précis, prédire le futur se ferait sans ambiguïté. Les systèmes dynamiques et aléatoires allaient prouver tout le contraire. Aujourd'hui, c'est tout le contraire.

Récemment, le théorème de Xavier Buff et Arnaud Chéritat prouve que le chaos est partout, qu'il est une règle générale de tous les systèmes dynamiques les plus simples qu'ils soient même dans une aire de calcul strictement positive et relativement simple.

Tout devient, du coup, imprévisible dans la compréhension du monde de la physique. Tout évolue de façon différente en fonction de paramètres, choisis et de leurs valeurs initiales.

Prévoir le temps, Henri Poincaré se rendit déjà compte que cela n'allait pas être simple vu le nombre de paramètres en météorologie. Qu'un système simple devienne une science avec des résultats complexes, là on passe à un problème d'échelle. Il était reconnu qu'une itération d'un nombre supérieur à un, au carré, l'envoie vers l'infini, inférieur à un et le résultat tend vers zéro. Rien de chaotique, rien de fractal, dans ces deux processus. Bien sûr.

Avec les nombres non réels, que l'on nomme comme complexes, au départ, on sort du linéaire pour couvrir tous les plans.

Depuis le début du 20ème siècle, les systèmes complexes ont intéressé pour tenter d'expliquer ce qui gouverne le chaos.

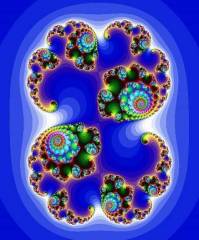Dès 1910, Pierre Fatou et Gaston Julia s'intéressent aux nombres complexes mais en limitant le calcul par une constante. Les ensembles de Julia à la recherche de l'orientation alternée entre l'infini et une  zone étroite obéissent déjà aux règles fractales, mais moins complexes car gardant le nombre "un" à l'intersection tout en versant déjà dans l'imprévisibilité du chaos. Recherche théorique. Pas de machine pour se le représenter dans la pratique à l'époque. L'avènement des PC en 1980 débloque cette impossibilité. Adrien Douady, et John Hubbard son élève, s'exercent pour donner une aire autre de déformations dans un jeu de symétries.

Prévoir le devenir par le calcul est le rêve qui attirait pour gagner aux jeux et en Bourse. Le mathématicien, Benoit Mandelbrot, employé chez IBM, s'y intéresse principalement dans ce sens.

L'ensemble de Mandelbrot permet une représentation en deux dimensions de ces fonctions de manière plane.

Depuis, les ordinateurs ont multiplié leur puissance de calcul de manière phénoménale. Aujourd'hui, le PC atteindrait les 2 milliards d'opérations par seconde rendant le travail de recherche et de test moins éprouvant pour les nerfs dans le temps d'attente.

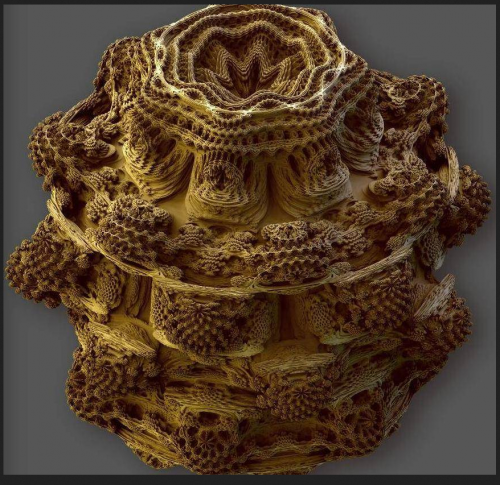
Sur le site de Daniel White, professeur de piano, les images du set de Mandelbrot sont passées récemment en trois dimensions. C'est tout simplement magique. Le désordre est conservé dans le complexe. Planète de l'imaginaire dans lequel un vaisseau spatial se perdrait en chemin dans un zooming sans fin au travers de labyrinthes.

John Hubbard, un des meilleurs spécialistes de cet ensemble Mandelbrot qui avait avait sorti le fameux dessin de cœur des fractales en deux dimensions et qui s'enchaînent du plus grand au plus petit détail de la même façon, en était émerveillé. L'astuce de ce "plus système dynamique non linéaire" avec un algorithme élémentaire constitué fut réalisé par le passage de nombres complexes au carré et en faisant jouer progressivement les couleurs dans le processus de calcul des points suivants.

Faire passer les calculs dans une 4ème dimension projetée sur un espace à trois dimensions, fut, d'abord, la solution proposée par Jean-François Colonna. Les nombres baptisés "quaternions" restaient toujours à base des opérations arithmétiques classiques.

Daniel White avec l'aide de Paul Nylander, transforma l'ensemble de Mandelbrot en passant à des exposants supérieurs au carré dans un processus itératif. Les détails apparurent plus intéressants au fur et à mesure qu'ils testaient les puissances supérieures. Exposant 8 semblait être le meilleur compromis. Les Mandel bulbes étaient nés en se référant à leur précurseur, Mandelbrot.

Il existait l'"éponge de Menger", plus ancienne, qui fut inventée en trois dimensions en 1926 par Karl Menger mais il est basé sur un autre principe : creuser un système de cubes en enlevant le centre par itération, qui ne suit pas la même logique fractale.

Mais à quoi ces Mandel bulbes peuvent-elles servir ?

Répondre "pour la beauté des yeux" serait un peu léger. La géométrie fractale permet d'aborder la complexité d'une rivière qui se perdrait dans ses méandres en reproduisant la même configuration tortueuse du départ. C'est vrai, le monde des fractales à base des nombres complexes en deux dimensions permettait déjà de reconstituer la nature, les feuilles d'un arbres, les nuages et bien d'autres choses du vivant. Les images numériques calculées point par point peuvent réduire considérablement les fichiers par la Loi de Zipf et de toutes les techniques qui tout en perdant de la définition permet de conserver une approximation honnête de l'image non compressée. Mais ce sont surtout les théories financières basée sur un modèle d'évolution des cours de la Bourse que la géométrie fractale prenait tout son sens dans la recherche.

En 2004, Mandelbrot publie "Une approche fractale des marchés" dans lequel il dénonce les outils mathématiques de la finance qu'il juge inadaptés. Très critique sur la théorie de Merton, Black et Scholes utilisée par les banques, car elle ne prend pas en compte les changements de prix instantanés et des informations essentielles, faussant ainsi les moyennes. Dès 1962, il signalait l'erreur d'appréciation en précisant que le hasard ne tenait pas compte de la sauvagerie de la Bourse sous-évaluant la fantaisie des évaluations et des indexes. D'après lui, les "sauts de Lévy" décriraient mieux les risques. Mais ceci est déjà une autre histoire et cette histoire-là va lui donner raison avec les crises.

Pour l'imagination, pas besoin d'utilité. Pas encore vu le site de Daniel White ? Évadez-vous, cela vaut le détour. Il y explique les techniques de ses multiples essais. En plus, quand on donne à ses résultats, des noms tel que "Retour du Chateau du Soleil couchant", "Rêves de solitude", ... il y a de quoi rêver.

Le chaos n'a pas encore dit son dernier mot.

Que ferait-on sans lui ? Réinventer l'ordre, c'est loin d'être plus sûr même pour les matheux.

L'enfoiré,

Sources principales, le Science & Vie de Février 2010

Les ensembles fractales en 2D existent encore sous d'autres formes.

Sur Agoravox, l'imagination en bulbes?

Citations:

• "Le monde est un chaos, et son désordre excède tout ce qu'on y voudrait apporter de remède.",Pierre Corneille
• "Le chaos est souvent source de vie alors que l'ordre génère des habitudes.", Henry Brooks Adams

30 août 2010: Le "Pour la Science de septembre" parle "Du relief dans les fractales". On passe, dans les fractales en 3D, à un besoin de force de calcul de 1000 fois supérieur. La formule f(z)=z2+c est une fonction quadratique qui passe des nombres réels aux nombres complexes. Dominic Rochon de l'Université du Québec à Trois-Rivières a créé le Tetrebrot qui rappelle étrangement un cristal de bismuth. Le britanique Tom Lowe se confronte avec "son monde" Mandelbox, volume cubique avec pliages et inversions qui ne s'échappent pas de l'infini. Du carré de z au carré, passer à z exposant 8, cela donne beaucoup d'idées

Un forum existe sur le sujet qui prend visiblement de l'extension.

24 janvier 2014 : Les fractales ont 40 ans. 

Le 12 février 1974, Mandelbrote annonce que le monde n'est plus lisse et qu'il dépend de l'échelle utilisée des instruments de mesure.

Les artistes s'en sont emparé, mais les scientifiques s'en sont peu souciés.

A quoi cela sert-il ?

Est-ce un effet de mode sans suite ?

Les fractales servent surtout à mesurer notre impuissance. 

Les murs anti-bruits, les catalyses fractales en archéologie pour analyser les clichés aériens, s'en sont servis.

Les fractales sont surtout là pour contrôler et prévoir l'évolution d'un système par des probabilités mais pas pour prévoir un événement à une certaine date.

Utilisé pour donner les chocs potentiel plus importants que prévus en économie, d'accord. Mais ce n'est pas une martingale. 

C'est là son moindre défaut.