Les secrets de nos pensées en équations mathématiques

Les maths et les sciences exactes ont, pour moi, moins d'erreurs à assumer que les sciences humaines. Il faut remonter à tellement de sources sociologique, psychologique pour obtenir un semblant de vérité ou de réalité à notre époque. Cela me donne quelques fois, un arrière-goût d'alexithymie seulement vaincue par l'humour.

Les concepts abstraits & énigmes des théories mathématiques n'ont pas ce problème sans être plus simples à comprendre pour autant. "Trop complexe le monde du numérique ?" demandais-je en 2012.
Pour décrire le monde extérieur, l'étonnante efficacité des mathématiques est à rechercher à l'origine dans ce langage numérique de manière plus précise et plus compacte que la manière analogique généralement utilisée.

Pour capturer notre monde intérieur, c'est par les lois de la nature dans le domaine des sciences du vivant ou du monde que Donald Glaser apporte aussi leurs déraisonnables efficacités pour représenter des choses qui, en elles-mêmes, ne représentent rien de concret.
Elles promettent de dévoiler le connectome et le cheminement de la moindre information jusqu'à révéler les secrets de son fonctionnements appliqués à la cognition.

...

Notre perception du temps

... est définie par une erreur logarithmique f(x)=ln(x).

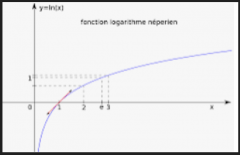La perception du temps se calcule par son logarithme naturel et népérien qui définit la puissance à laquelle il faut élever e pour obtenir x. Elle est donc la bijection réciproque de la fonction exponentielle.
A cause des erreurs de nos neurones compteurs de temps, le temps perçu n'est pas le même et évolue en pente douce.
Plus le temps à comptabiliser est long, plus le rapport entre l'erreur et le temps effectif sera petit quand l'intervalle de temps réel est grand.
Rien à voir avec la somme de toutes les inexactitudes voulues linéaires.
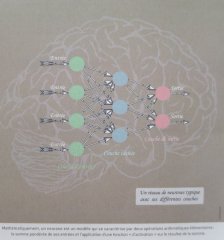
Le pacemaker-accumulateur cardiaque qui envoie des impulsions à intervalles réguliers doit en tenir compte pour ne pas essouffler son utilisateur en reproduisant les erreurs de l'horloge interne.
"Ces neurones ne sont que des métaphores qui permettent de comprendre ce qui se passe et la relation avec les logarithmes", Quentin Hallez. Dix minutes à attendre "bêtement" et impatiemment paraissent plus longues que 10 minutes dans l'excitation du déroulement de quelque chose qu'on n'attend pas avec le risque de surestimer le temps réel d'une opération. Les neurones artificiels, plus évoluées, en tiennent compte par leur capacités cognitives en entrée et infère la perception selon le contexte. Intégrer la mémoire, l'attention, la plasticité cérébrale et la récurrence dans le réseau neuronal permet par la une couche intermédiaire de retourner à l'entrée pour coller avec la perception logarithmique du temps en fonction de la durée. Il faut faire intervenir les théories mathématiques associées aux réseaux de neurones pour trouver l'inspiration dans le monde de la biologie, des lois de la génétique et de l'évolution naturelle avec pour objectif de répliquer la tolérance à la faute et la faculté d'apprendre des systèmes biologiques des informations des neurones formels en axiones connectés aux dendrites par les synapses pour obtenir la somme des entrées pondérées et leur activation linéaire, de seuil, radiale ou stochastique et à la sortie, les représenter par un graphe d'objets élémentaires dont la théorie a été initiée pour répondre à des questions d'optimisation de la connexité entre un sommet et un autre selon Euler.

Le lemme d'Ito est un processus stochastique et donc aléatoire qui dépend du temps peut décrire son évolution à l'aide d'équations différentielles, défini par la notion d'intégrale du mouvement brownien comme véritable clé de voute du calcul aléatoire et qui a trouvé dans la finance l'une des plus pertinentes applications.
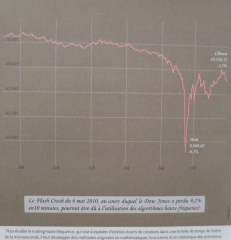
Depuis l'apparition de l'informatique et de la puissance phénoménale de calcul des ordinateurs, les mathématiques financières ont permis de comprendre les opportunités et les risques par des algorithmes de Trading Haute Fréquence pour modéliser la microstructure du marché en tenant compte du prix des actifs, des volumes échangés et du nombre d'acteurs par des tendances jusqu'aux microsecondes. Les "flash-crash" sont heureusement contrôlés par le "tick" représentant le plus petit écart type autorisé sur une cotation. 

...

La restauration de la mémoire de façon exponentielle

La disparition de la mémoire de travail avec sa force de déclin (D) montre une courbe associée avec l'évolution mnésique suite à l'apprentissage d'une tâche. f(t)= e exp -Dt alternant avec une distraction, une restauration, une autre distraction et une autre restauration plus faible que la précédente.
Lors de faire les courses, la mémorisation des différentes choses à rapporter est, si on n'en prend pas note, dépendante de la mémoire et de l'importance de ce qu'on considère personnellement d'important. La perte de mémoire se poursuit inversement proportionnelle à la fonction exponentielle et en fonction des distractions. Notre système cognitif se détériore en plus avec l'âge. Le maintien d'une information et de son traitement font des allées et venues entre mémoire et réalisation d'une tâche à la rencontre d'éléments perturbateurs qui existent en fonction de la proportion du temps nécessaire à sa réalisation, multiplié par le nombre de récurrences et divisé par le temps alloué pour l'exécuter en capturant l'attention. Le cerveau fonctionne en séquentiel et en aléatoire plus il y a de distractions qui vont faire perdre les objectifs initiaux dans une pente exponentielle inversée f(t)=exp(-Dt). La réactivation de la mémoire coïncide avec la fonction exponentielle.

...

L'attention est une courbe en cloche

L'attention est dépendant de beaucoup de facteurs souvent personnels. Modéliser cela demande de les introduire parfois artificiellement si on ne connait pas la personne. Le processus cognitif de l'attention est difficile à caractérisé. Pourtant il guide l'immense majorité de nos comportements et s'exprime sous de multiples facettes auditives pu visuelles. Les propriétés des mathématiques semblent parfaitement appropriées pour les aborder avec efficacité. 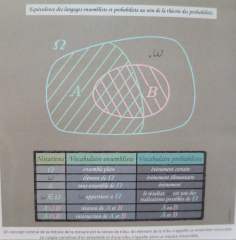L'attention visuelle commence par le domaine des probabilités. Un détail focalisé peut perturber ou améliorer complètement l'aspect général d'un object ou d'un visage à courte distance alors que l'on perd cette attention par des contacts virtuels sous internet. L'attention est comme un filtre qui suit une courbe gaussienne. Les informations sensorielles se réduisent selon une pente de plus en plus floue en fonction de la distance. Le son par une musique de fond peut perturber l'attention en alternance avec le côté visuel. Le "shift attentionnel" est décrit par les équations de Lotka-Volterra pour modéliser la fluctuation des populations animales en fonction des ressources disponibles. 

...

Une double intégrale mathématique prend part dans nos décisions

Pour prendre une décision en Bourse, il y a deux options ou notions à prendre en considération pour maximiser les gains ou limiter les pertes.
Prendre un pari risqué mais potentiellement payant.
Appliquer le programme pour s'assurer une note moyenne.
Une fonction en double intégrale liées aux probabilités du théoricien Thomas Bayes qui tente d'y répondre par la représentation d'un triangle.
La théorie des probabilités étudie les lois du hasard.
La théorie des jeux s'est développée autour des questions économiques sous l'impulsion de John Nash pour aborder les questions de stratégie.
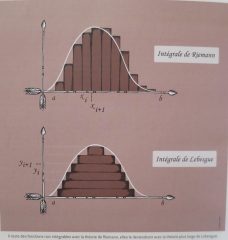
La théorie de la mesure intégrale est à l'origine de la théorie de l'intégration avec la forme moderne des travaux de Riemann la plus aboutie de Lebesgue à la prolongation de la longueur à la surface.
Ce n'est pas uniquement par la connaissance du monde à savoir son état mais aussi un lien à la psychologie qui veille par une fonction de la vraisemblance de l'objectif à atteindre.
La situation globale actuelle décrypte et attribue un score.
L'antériorité de cette situation, un deuxième score.
Les habitudes du décideur, un troisième score qu'une double intégrale se présente pour évaluer la pertinence d'une décision par la théorie des modèles intégrée à la partie sémantique de la logique, de la théorie des groupes et des théorèmes de complétude et de capacité.
Un modèle de décision peut être le même dans beaucoup d'autres situations en recourant à des préférences personnelles et par la subjectivité avec un coefficient d'erreur acceptable.

...

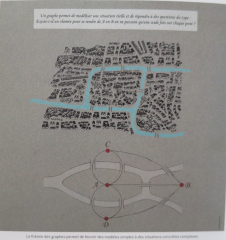
La perception de l'espace entre deux géométries

Le 5ème postulat de la géométrie d'Euclide expose qu'entre un point et un autre, il n'existe qu'une droite parallèle à celle-ci à partir d'un pont donné.
L'intuition de la géométrie de Riemann a introduit une forme de métrique pour étudier les propriétés des espaces courbes utilisés en relativité générale.
Le postulat d'une autre géométrie antagoniste dite "hyperbolique" dit que les droites se courbent jusqu'à se recroqueviller à longue distance.
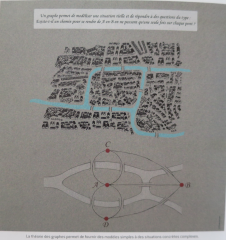
Des expériences réentes prouvent que la géométrie hyperbolique est plus réaliste par la représentation de l'espace que fait le cerveau et de lui-même en un formidable terrain de jeu mathématique. Cela permettrait de comprendre l'efficacité du cheminement de l'information par les matrices, et les équations différentielles comme un objet ellipsoïdal en 3 dimensions mis en équations pour être modélisé avec ses pensées.
L'imagerie médicale réalise un maillage de la surface du cerveau au lieu de le représenter sa forme par l'expansion tangentielle du cortex en quantifiant ses circonvolutions par une caractérisation de sa morphologie à associer aux symptômes pathologiques. Cet instrument de diagnostic fait progresser les neurosciences.
C'est là que la théorie des graphes dans leur structure reliant des nœuds constitués par des neurones et des arêtes constituées par des axones, intervient comme une matrice de connectivité numérique faite dans des cases construites de 0 ou de 1 mis en réseaux.

...

Réflexions du Miroir

Beaucoup de théories de mathématiciens pour révéler l'étonnante efficacité des mathématiques. La déraisonnable efficacité des mathématiques pour décrire la nature se retrouve dabs la capture de notre monde intérieur par le cheminement de la moindre information jusqu'au secret intime de son fonctionnement appliqué à la cognition.
Pour Aristote, les mathématiques dérivent de notre perception du monde intrinsèquement humaines.
Pour Platon, elles existeraient dans le monde des idées, hors de l'esprit humain pour tenter d'y ressembler.
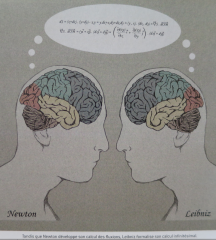
Le calcul infinitésimal, né vers la fin du 17ème siècle par les cerveaux de Newton et de Leibniz.
La suite de Fibonnacci ne serait qu'une suite logique à une pensée et un socle sur lequel repose la réalité.
Une fonction exponentielle décrit l'évolution d'une pandémie et les fonctionnements de la mémoire. Une équation différentielle permet de décrire l'évolution des populations et un mécanisme de l'attention. La géométrie hyperbolique s'applique à la lumière de l'espace-temps et de l'espace de l'Univers entier.
En 1961, la théorie du chaos découverte pas hasard par Lorenz, permet de décrire des systèmes en évolution en introduisant la notion imprédictibilités de systèmes déterministes de la croissance de l'incertitude par le biais de la sensibilité ressemblant aux ailes déployées d'un papillon. En 1971, Takens qualifie cette figure d'attracteurs étranges dont les dimensions sont fractales.
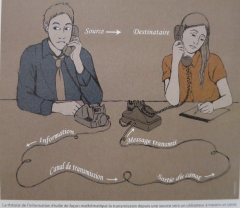
La théorie de l'information qui mène au stade de l'intelligence artificielle a été formalisée par Claude Shannon dans les années 1940.
Nous sommes donc 80 ans après avec la théorie de la communication sur Internet entre une source et un destinataire par un canal de transmission qui se produit via un concept d'entropie dans l'espérance de la variable binaire aléatoire 1 et du 0 entre interlocuteurs, converti dans un langage humain à la vitesse de la lumière dans une bande passante au risque d'en faire une usine à gaz. Grâce au développement d'une théorie mathématique, il existe une révolution silencieuse par la mathématisation de la conscience comme un grand défi des neurosciences et des sciences cognitives émergeant de la fusion de toutes nos perceptions sensorielles, pensées et actions modélisables à quantifier la valeur intrinsèque de toutes nos expériences subjectives à plusieurs dimensions.
Si les maths ne vous semblent pas belles, ce serait le moment de retourner aux fractaels que je décrivais déjà en 2020 dans "Des bulbes pour l'imagination"..
A coups de modélisations computationnelles, la pensée s'éclaire. Les fonctions exponentielles de notre mémoire se forment en équations différentielles dans le mécanisme de l'attention qu'il ne faut pas confondre avec la concentration qui se détruisent l'une l'autre. La géométrie hyperbolique se retrouve dans notre perception de l'espace. La description du cerveau, elle-même, par le gommage des particularités interindividuelles.

En résumé, les mathématiques peuvent décrire n'importe quoi.
Le cerveau est mathématique avec ou sans l'encéphale. Mis en équations par l'imagerie médicale et par l'expansion tangentielle du cortex en circonvolutions, le cerveau est étudié par les neurosciences avec la cartographie du connectome tout en devenant l'enjeu de l'IA.

Si vous désirez aller plus loin dans les maths, faites des voyages au pays des maths.

Il vaut le détour, même si ses abords semblent difficiles d'accès. On y parle une langue bizarre, pleine de polytopes, de variétés différentielles, de nombres transfinis. On y trouve aussi des paysages épiques, des idées vertigineuses et même des choses utiles !  Visite inédite dans toutes les dimensions  et les recoins de ce pays... guidée, bien sûr !

Il est repris dans le commentaire qui suit.

...

Humour de matheux

1. Erreur de logique du syllogisme de la règle des signes !
Les amis de mes amis sont mes amis.
Les amis de mes ennemis sont mes ennemis.
Les ennemis de mes amis sont mes ennemis.
Les ennemis de mes ennemis sont mes amis.

2. "Chaque fois que je vois le nombre 1, j'ai envie de l'aider à s'échapper... Il a constamment à ses trousses, derrière, le zéro qui veut le rattraper et devant, toute la mafia des grands nombres qui le guettent, Romain Gary

3. "Les maths, c'est comme l'amour. Une idée simple mais qui peut parfois se compliquer", Robert Drabek

4. "L'amour c'est comme l'arithmétique : ça commence par un bizou, on s'envoie Euler dans Lagrange et ça finit par des Gauss"

5. "Géométrie politique : le carré de l'hypoténuse parlementaire est égal à la somme de l'imbécilité construite sur ses deux côtés extrêmes", Pierre Dac

6. Mon instinct m'oblige à égaliser le débit et le crédit pour obtenir un bilan correct alors qu'il n'existe aucun argument seulement positif ou équitablement négatif", Réflexion du Miroir.  

Pas d'accord avec les théories des maths ?

Passez alors à celles des photos de la myth-ologie,  de la psyhologie et de la sociologie.

Le "pipigate", par exemple, peut-être une histoire secrète des mots vedettes, expliquée d'abord
.

Repris par le pipigate du cactus, on est loin des maths mais n'est-ce pas normal dans le pays de Manneken Pis ?
.

Mais nous avons des cours EVRAS dont le Cactus en fait la pub 
.

Le pipi ferait-il un grand bond en avant avec les équations mathématiques en considérant qu'il soit bon d'avant à partir de l'arrière ? 

PS : Préversion de ce billet sur agoravox.fr

Le nouveau Rollings Stones est une bonne façon de sortir des maths... 

Allusion

...

Y a-t-il quelqu'un qui voudrait jouer au bowling avec Jean-Luc Foncq

30/10/2024 : Les mathématiques sont partout dans la nature. Dans son livre, "Une mathématicienne au jardin", Claire Lommé aborde les notions mathématiques de base par le prisme de la nature. Nul besoin d'être un savant, un as du calcul ou un géomètre. Il suffit d'avoir le goût de la fl ânerie, de la liberté, et puis surtout... d'être curieux 

Blog : Pierre carrée

5/12/2024: au 28' parle des Maths

La Théorie des ensembles  et Georges Papy 

n'ont pas été évoqués.

Un retour au cours s'impose